rhea use a venn diagram to sort shapes what label could she use for circle a
Venn Diagrams
In this topic you will acquire how to construct a Venn diagram and and so how to utilize a Venn diagram to determine probabilities. Make certain you are happy with the post-obit topics before standing.
- Basic Probability
- Fractions, Decimals and Percentages
Level 4-5 GCSE 



Drawing Venn Diagrams
A typical Venn diagram looks similar the pic below. A Venn diagram is a style of grouping different parts of information known every bit sets . Drawing Venn diagrams is relatively simple as shown beneath.
Example: We have the numbers \{ane, ii, 3, iv, v, half-dozen, 7, 8, 9, x, 11\}.
Put the odd numbers in A and prime numbers in B. Depict a Venn diagram for this data.
Footstep 1: Identify numbers that are odd: \{1, \, 3, \, 5, \, vii, \, 9, \, 11 \} and numbers that are prime number: \{ii, \, 3, \, 5, \, 7, \, 11 \}. There's some crossover here: \{3, \, 5, \, 7, \, 11\} are contained in both , which means they go in the intersection.
Step 2: Numbers that are odd merely aren't prime: 1 and 9. These will go in the part of department A that doesn't intersect with B.
Numbers that are prime only aren't odd: 2. These will get in the part of circle B that doesn't intersect with A.
Footstep 3: All the numbers that are neither odd nor prime number: four, 6, viii, and 10, volition go inside the rectangle but outside either circle.
The consequence is the Venn diagram shown.
Level 4-5 GCSE 



Interpreting Venn Diagrams
We can utilise Venn diagrams to solve probability problems.
Instance: In the Venn diagram below, A contains odd numbers and B contains prime numbers.
A number is selected at random. Use the Venn diagram to determine the post-obit:
a) The number selected is both odd and prime.
Looking at the Venn diagram, we see that 4 of the 11 numbers are in both A and B, so the probability of a number being both odd and prime is, \dfrac{4}{11}.
b) The number selected is odd and isn't a prime number.
We are looking for all numbers that are in set A but non ready B, 1 and 9, which gives a probability of, \dfrac{2}{11}
Level four-v GCSE 



Level 8-nine GCSE 



Venn Diagrams and Conditional Probability
Venn diagrams tin as well exist used to solve provisional probability problems.
Example: In the Venn diagram below, Thousand represents students selecting Geography and H represents students selecting History. Apply the Venn diagram to determine \text{P}(Yard \text{ given } H) (Also written \text{P}(G|H)).
Nosotros desire to find the probability that someone takes Geography given that we already know they take History. If nosotros know someone takes History, and then they must exist one of the 2+12=14 people. And then, there are 12 out of those 14 people who take Geography, or in other words
\text{P}(One thousand|H)=\dfrac{12}{14}
Level 8-9 GCSE 



Case Questions
a) The outset thing we need to do is draw a rectangle labelled \xi to represent all the year 9 students. And so nosotros demand to draw two circles which overlap, i labelled 'football' and the other labelled 'rugby'.
There is some elementary information which we can input immediately. We are told that 14 students do not play rugby or football, and so nosotros tin can write '14' exterior the circles, simply still inside the rectangle. We are also told that 42 students play both sports, and then we can write '42' in the intersection of the two circles.
The only information which nosotros need to complete is the number of students who play football only and the number of students who play rugby only. Since in that location are 126 students in total, of which 14 play neither sport and of which 42 play both sports, nosotros can work out how many students play football game or rugby but:
126-42-14 = 70\text{ students}
At present that we know that a total of 70 students play only football or only rugby, we are now in a amend position to work out exactly how many students fall into each category. Nosotros are told that the ratio of the number of students who play football but to the number of students who play rugby just is 7 : 3. This ways that \frac{vii}{10} of the 70 students play football only and \frac{3}{10} of the 70 students play rugby simply. (We are dealing in tenths here because the sum of the ratio is 10.).
The number of students who play football game but can exist calculated as follows:
\dfrac{vii}{10}\times70 = 49\text{ students}
The number of students who play rugby merely can exist calculated equally follows:
\dfrac{3}{10}\times70 = 21\text{ students}
Therefore we need to insert '49' inside the football game circle (but not in the intersection) and '21' within the rugby circle (but not in the intersection).
Our completed Venn diagram should be similar to the beneath:
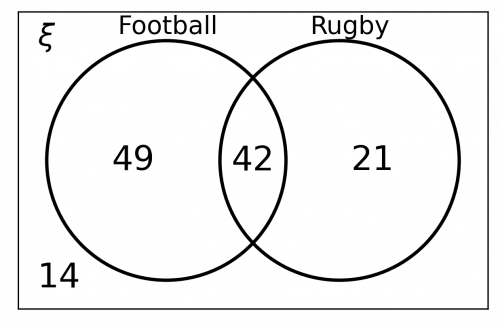
b) We know that 21 students play rugby only out of the total 126 students. We tin can write this as the following fraction:
\dfrac{21}{126}
This fraction tin can be simplified to:
\dfrac{1}{six}
a) The number of students in year x is the total of:
- All the students that study geography simply (40)
- All the students that written report history only (52)
- All the students that study both geography and history (fourteen)
- All the students that written report neither history nor geography (36)
xl+52+fourteen+36=142\text{ students}
b) We know that there are 142 students in total and, of these, 14 report both history and geography. Nosotros can express this as the post-obit fraction:
\dfrac{14}{142}
This fraction can exist simplified to:
\dfrac{seven}{71}
(You could give the probability as a decimal or as a percentage (the question doesn't state how the answer should be given), only since both the decimal (0.0985….) and the percent (9.85…\%) accept several decimal places, leaving the probability as a fraction would probably exist the virtually sensible option here, but the decimal and per centum answers are not incorrect.)
c) The phrase 'given that the student selected does not written report geography' tells us that we demand to work out how many students practice non study geography. The students that don't study geography are those who report history merely (52 students) or those who study neither subject (36 students). The total that do not study geography is therefore 52+36 = 88 students.
Of these 88 students, nosotros demand to find how many do not study history. The 36 that report neither subject are the ones that do not study history, so 36 out of the 88 who do not report geography practice not study history. We can write this equally the following fraction:
\dfrac{36}{88}
This fraction can be simplified to:
\dfrac{xviii}{44}
This fraction can be simplified again to:
\dfrac{9}{22}
(The decimal answer of 0.409….. or the per centum answer of 40.909….\% are both acceptable ways to express the probability likewise.)
a) What demand to input the information. Some of the data we are going to input will exist easy, other parts may be more than confusing. Let's start with i fact at a time:
- All \bf{eighty} students like at to the lowest degree \bf{1} of the animals. There is non much nosotros can practice with this data. However, this is a cardinal piece of information since it tells united states that once nosotros accept filled in the Venn diagram, the numbers should add up to 80.
- \bf{fifteen} students like all \bf{3} animals. If 15 students like all three animals, then nosotros can insert '15' in the intersection of all 3 circles.
- \bf{14} students similar sharks and crocodiles merely practice not like hippos. With this information we can insert '14' in the section where sharks and crocodiles intersect (which should exist outside the hippos circle).
- \bf{23} students similar crocodiles and hippos. This is the piece of data which can cause confusion. Although that statement says that 23 students like crocodiles and hippos, this doesn't mean that 23 students like crocodiles and hippos only. This figure of 23 also includes students who like sharks every bit well every bit crocodiles and hippos. This is the slightly confusing role of the question! 15 students like sharks, crocodiles and hippos, then that means that these 15 students definitely like crocodiles and hippos. So, if at that place are 23 students in total who like crocodiles and hippos, that means that at that place are viii students who like crocodiles and hippos but. Therefore we can now insert '8' in the intersection of crocodiles and hippos (but not in the intersection of sharks, crocodiles and hippos). Y'all may need to read this paragraph a few times: it volition sink in and make sense eventually!
- \bf{21} students like sharks and hippos. This is a very like piece of information to the above piece of data about crocodiles and hippos. 15 students similar sharks, crocodiles and hippos, therefore that means that in that location are at to the lowest degree 15 students who like sharks and hippos. Since we have been told that the total number of students who like sharks and hippos is 21, and so this means that half dozen students like sharks and hippos, but not crocodiles. Therefore we can insert 'six' in the intersection of sharks and hippos.
- \bf{44} students like crocodiles. We know that 14 students like crocodiles and sharks, that 15 students like sharks, crocodiles and hippos, and that a farther eight that like crocodiles and hippos, so if we add these numbers upwards we know that 37 students like crocodiles. Since we are told that 44 students similar crocodiles in total, this means that there are 7 students who like crocodiles merely. Therefore we tin insert '7' in the office of the crocodile circle that does not overlap with any other section.
- \bf{12} students just like sharks. All we demand to practise is insert '12' in the sharks only section.
All we need to practise is work out how many students but like hippos. We know that in that location are 80 students in total, and nosotros accept filled in every section of the Venn diagram except this final hippos but section. If nosotros decrease all of the numbers from our total of fourscore, we volition be able to piece of work out how many students only like hippos:
fourscore-12-14-vii-6-15-eight=eighteen
Therefore our completed Venn diagram will look similar to the below:
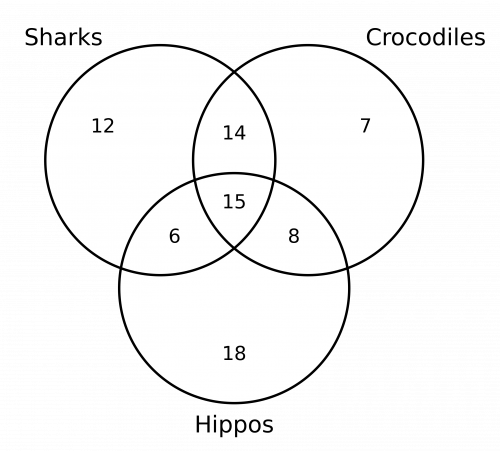
b) At that place are eighty students in total, of which xviii but like hippos. This means that eighteen out of the 80 simply like hippos which can be written as the following fraction:
\dfrac{eighteen}{80}
This fraction tin can be simplified to:
\dfrac{9}{40}
So, the probability of a person being selected at random and simply liking hippos is \frac{9}{xl} (or nine\div40=0.225 if yous adopt to give your answer every bit a decimal. The answer of 22.five\% is as well acceptable.)
c) There are 44 students in full that like crocodiles. There are 14 students that like crocodiles and sharks and eight students that like crocodiles and hippos, then in that location are 22 students that similar crocodiles and ane other fauna.
This ways that 22 out of the 80 only similar crocodiles and one other type of animal, which can be written as the post-obit fraction:
\dfrac{22}{lxxx}
This fraction can be simplified to:
\dfrac{eleven}{40}
Then, the probability of a person beingness selected at random and only liking hippos is \frac{11}{twoscore} or xi\div40=0.275 if you prefer to requite your respond as a decimal. The answer of 27.5\% is also acceptable.
Related Topics
Worksheet and Example Questions
Drill Questions
Source: https://mathsmadeeasy.co.uk/gcse-maths-revision/venn-diagrams/
0 Response to "rhea use a venn diagram to sort shapes what label could she use for circle a"
Post a Comment